Алгоритм ДейкстрыНеплохой такой алгоритм, я его в дипломе использовала для 3D навигации по универу. Ищет кратчайший путь до заданного объекта от начальной точки.
Неформальное объяснение» Кликните сюда для просмотра оффтоп текста.. «
Каждой вершине из V сопоставим метку — минимальное известное расстояние от этой вершины до a. Алгоритм работает пошагово — на каждом шаге он «посещает» одну вершину и пытается уменьшать метки. Работа алгоритма завершается, когда все вершины посещены.
Инициализация. Метка самой вершины a полагается равной 0, метки остальных вершин — бесконечности. Это отражает то, что расстояния от a до других вершин пока неизвестны. Все вершины графа помечаются как непосещённые.
Шаг алгоритма. Если все вершины посещены, алгоритм завершается. В противном случае, из ещё не посещённых вершин выбирается вершина u, имеющая минимальную метку. Мы рассматриваем всевозможные маршруты, в которых u является предпоследним пунктом. Вершины, в которые ведут рёбра из u, назовем соседями этой вершины. Для каждого соседа вершины u, кроме отмеченных как посещённые, рассмотрим новую длину пути, равную сумме значений текущей метки u и длины ребра, соединяющего u с этим соседом. Если полученное значение длины меньше значения метки соседа, заменим значение метки полученным значением длины. Рассмотрев всех соседей, пометим вершину u как посещенную и повторим шаг алгоритма.
ПримерРассмотрим выполнение алгоритма на примере графа, показанного на рисунке. Пусть требуется найти кратчайшие расстояния от 1-й вершины до всех остальных.
Кружками обозначены вершины, линиями — пути между ними (ребра графа). В кружках обозначены номера вершин, над ребрами обозначена их «цена» — длина пути. Рядом с каждой вершиной красным обозначена метка — длина кратчайшего пути в эту вершину из вершины 1.
Первый шаг. Рассмотрим шаг алгоритма Дейкстры для нашего примера. Минимальную метку имеет вершина 1. Её соседями являются вершины 2, 3 и 6.
Первый по очереди сосед вершины 1 — вершина 2, потому что длина пути до неё минимальна. Длина пути в неё через вершину 1 равна сумме кратчайшего расстояния до вершины 1, значению её метки, и длины ребра, идущего из 1-й в 2-ю, то есть 0 + 7 = 7. Это меньше текущей метки вершины 2, бесконечности, поэтому новая метка 2-й вершины равна 7.
Аналогичную операцию проделываем с двумя другими соседями 1-й вершины — 3-й и 6-й.
Все соседи вершины 1 проверены. Текущее минимальное расстояние до вершины 1 считается окончательным и пересмотру не подлежит (то, что это действительно так, впервые доказал Э. Дейкстра). Вычеркнем её из графа, чтобы отметить, что эта вершина посещена.
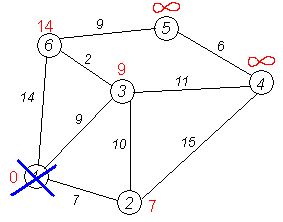
Второй шаг. Шаг алгоритма повторяется. Снова находим «ближайшую» из непосещенных вершин. Это вершина 2 с меткой 7.
Снова пытаемся уменьшить метки соседей выбранной вершины, пытаясь пройти в них через 2-ю вершину. Соседями вершины 2 являются вершины 1, 3 и 4.
Первый (по порядку) сосед вершины 2 — вершина 1. Но она уже посещена, поэтому с 1-й вершиной ничего не делаем.
Следующий сосед вершины 2 — вершина 3, так как имеет минимальную метку из вершин, отмеченных как не посещённые. Если идти в неё через 2, то длина такого пути будет равна 17 (7 + 10 = 17). Но текущая метка третьей вершины равна 9<17, поэтому метка не меняется.
Ещё один сосед вершины 2 — вершина 4. Если идти в неё через 2-ю, то длина такого пути будет равна сумме кратчайшего расстояния до 2-й вершины и расстояния между вершинами 2 и 4, то есть 22 (7 + 15 = 22). Поскольку 22<\infty, устанавливаем метку вершины 4 равной 22.
Все соседи вершины 2 просмотрены, замораживаем расстояние до неё и помечаем её как посещенную.
Третий шаг. Повторяем шаг алгоритма, выбрав вершину 3. После её «обработки» получим такие результаты:
Дальнейшие шаги. Повторяем шаг алгоритма для оставшихся вершин. Это будут вершины 6, 4 и 5, соответственно порядку.
Завершение выполнения алгоритма. Алгоритм заканчивает работу, когда нельзя больше обработать ни одной вершины. В данном примере все вершины зачеркнуты, однако ошибочно полагать, что так будет в любом примере - некоторые вершины могут остаться незачеркнутыми, если до них нельзя добраться. Результат работы алгоритма виден на последнем рисунке: кратчайший путь от вершины 1 до 2-й составляет 7, до 3-й — 9, до 4-й — 20, до 5-й — 20, до 6-й — 11.
» Кликните сюда для просмотра оффтоп текста.. «
Поиск кратчайшего пути между двумя вершинами в графе.
Реализация на основе очереди с приоритетами. Сложность порядка O(nlog(n)).
Цитата
#include <iostream>
#include <set>
#include <vector>
using namespace std;
typedef vector<int> vi;
typedef pair<int,int> ii;
typedef vector<ii> vii;
typedef vector<vii> vvii;
const int MAX = 1001;
const int MAXINT = 1000000000;
int n;
vvii G(MAX);
vi D(MAX, MAXINT);
void Dijkstra(int s)
{
set<ii> Q;
D[s] = 0;
Q.insert(ii(0,s));
while(!Q.empty())
{
ii top = *Q.begin();
Q.erase(Q.begin());
int v = top.second;
int d = top.first;
for (vii::const_iterator it = G[v].begin(); it != G[v].end(); it++)
{
int v2 = it->first;
int cost = it->second;
if (D[v2] > D[v] + cost)
{
if (D[v2] != 1000000000)
{
Q.erase(Q.find(ii(D[v2], v2)));
}
D[v2] = D[v] + cost;
Q.insert(ii(D[v2], v2));
}
}
}
}
int main()
{
//freopen("input.txt", "r", stdin);
//freopen("output.txt", "w", stdout);
int m, s, t = 0;
scanf("%d %d %d %d", &n, &m, &s, &t);
for (int i = 0; i < m; i++)
{
int a, b, w = 0;
scanf("%d %d %d", &a, &b, &w);
G[a - 1].push_back(ii(b - 1, w));
G[b - 1].push_back(ii(a - 1, w));
}
Dijkstra(s - 1);
printf("%d\n", D[t - 1]);
return 0;
}
» Кликните сюда для просмотра оффтоп текста.. «
Цитата
//* uGraph - модуль для работы с графами - алгоритмы на графах
unit uGraph;
interface
uses
uPath;
type
TVertex = record
id : Integer;
x,y,z : Single;
Tag : Integer;
Marked : Boolean;
DistFromStart : Single;
PrevVertex : Integer;
end;
TGraph = class
public
//* Public declarations
M : array of array of Single;
V : array of TVertex;
N : Integer;
Path : TPath;
//*
StartVertex : Integer;
FinishVertex : Integer;
//*
constructor Create;
procedure LoadGraph (const FileName : ShortString);
procedure FindPath (const Tag : Integer );
end;
implementation
//* TGraph *//
procedure TGraph.LoadGraph(const FileName: ShortString);
var
F : TextFile;
i,j : Integer;
begin
AssignFile (F, FileName);
Reset (F);
ReadLn (F, N);
SetLength (M, N, N);
SetLength (V, N);
//
for i := 0 to N-1 do
begin
ReadLn (F, V[i].x, V[i].y, V[i].z, v[i].tag);
StartVertex := 0;
end;
for i := 0 to N-1 do
for j := 0 to N-1 do
begin
try
Read (F, M[i,j]);
except
M[i,j] := 10000000;
end;
end;
//
CloseFile (F);
end;
procedure TGraph.FindPath(const Tag: Integer);
var
i,j : Integer;
NotMarked : Integer;
vm,pv : Integer;
MinDist : Single;
begin
for i := 0 to N-1 do
begin
v[i].Marked := False;
v[i].DistFromStart := M[StartVertex,i];
if M[StartVertex,i] = -1 then
v[i].DistFromStart := 10000000;
v[i].id := i;
if v[i].Tag = Tag then FinishVertex := i;
end;
//*
v[StartVertex].Marked := True;
v[StartVertex].PrevVertex := -1;
NotMarked := N-1;
while NotMarked <> 0 do
begin
MinDist := 10000000;
for i := 0 to N-1 do
if (not v[i].Marked) and (v[i].DistFromStart < MinDist) and (v[i].DistFromStart <> -1) then
begin
vm := i;
MinDist := v[i].DistFromStart;
end;
v[vm].Marked := True;
NotMarked := NotMarked-1;
for i := 0 to N-1 do
if not v[i].Marked then
if (v[i].DistFromStart > v[vm].DistFromStart+M[vm,i]) and
(v[i].DistFromStart <> -1) and (v[vm].DistFromStart <> -1) and
(M[vm,i] <> -1) then
begin
v[i].DistFromStart := v[vm].DistFromStart+M[vm,i];
v[i].PrevVertex := vm;
end;
end;
//*
pv := v[FinishVertex].PrevVertex;
Path.Clear;
Path.AddVertex (v[FinishVertex].x, v[FinishVertex].y, v[FinishVertex].z, v[FinishVertex].Tag);
while pv <> -1 do
if pv <> -1 then
begin
if v[pv].PrevVertex <> -1 then
Path.AddVertex (v[pv].x, v[pv].y, v[pv].z, v[pv].tag);
pv := v[pv].PrevVertex;
end;
//*
end;
constructor TGraph.Create;
begin
Path := TPath.Create;
end;
end.
Коллекция алгоритмов, в помощь начинающим
4.01.2010 - 14:21
2880 
Соловей Коллекция алгоритмов 4.01.2010 - 14:21
